Introducción
En mi análisis anterior sobre MathCanvas, mi conclusión fue: La inestabilidad de los modelos grandes en geometría no se debe a que no entiendan la imagen, sino a que no tienen una estructura intermedia estable sobre la que operar.
Algunos trabajos comenzaron a hacer que el modelo dibuje primero y razone después.
Por ejemplo, MathCanvas hace que el modelo genere bocetos internos y luego razone sobre ellos.
Después de ese artículo, un lector me preguntó:
Si los pasos visuales intermedios son tan importantes, ¿por qué no dejar que el modelo dibuje la figura de verdad?
Busqué investigaciones relacionadas y sí existe: CodePlot-CoT de HKU.
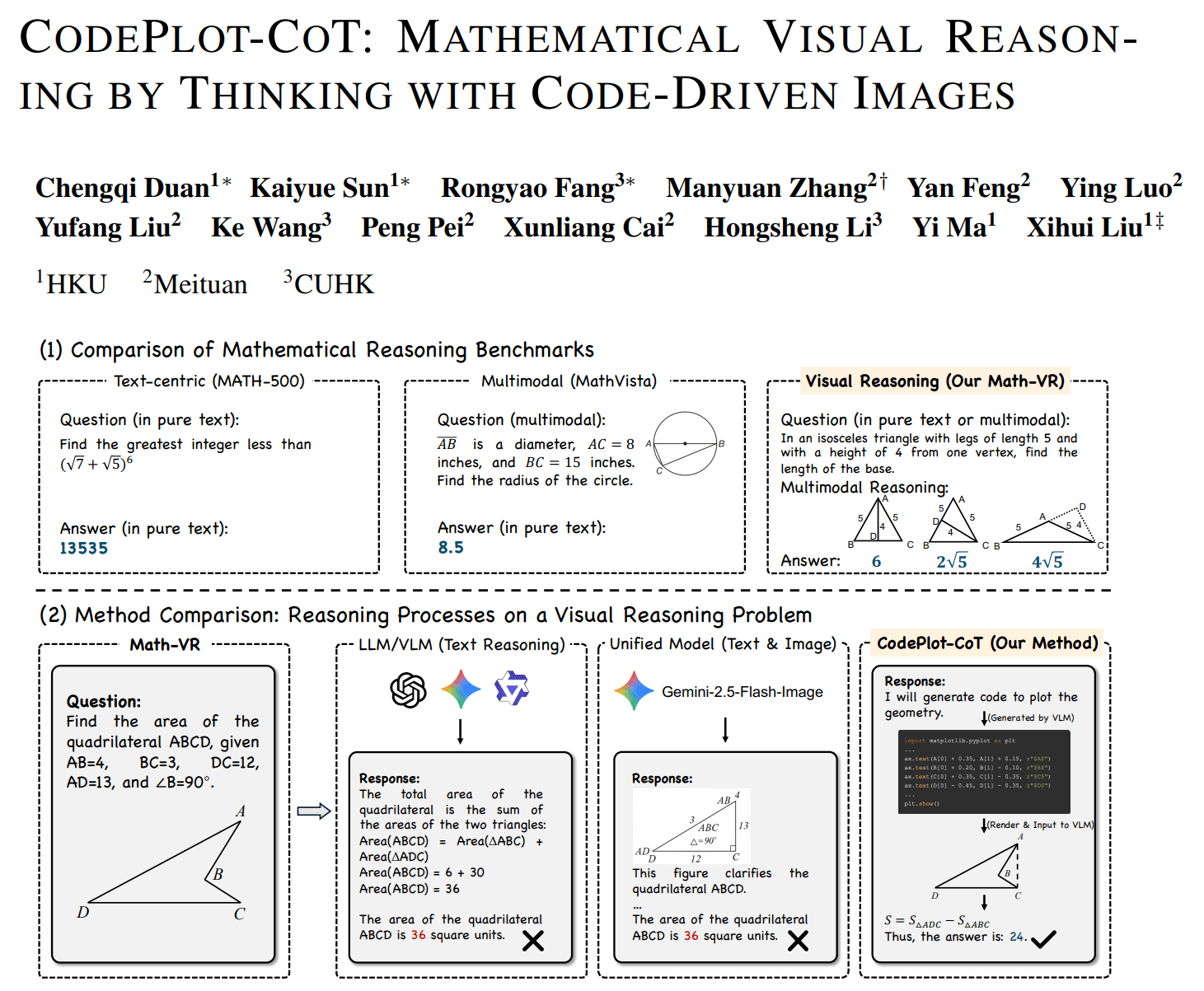
El modelo deja de "imaginar" líneas auxiliares y escribe Python con matplotlib para trazarlas explícitamente antes de seguir resolviendo.
Suena razonable: si el razonamiento visual es inestable, dale al modelo un mundo visual ejecutable.
Pero aparece una pregunta nueva:
Cuando el modelo empieza a escribir código gráfico, ¿está haciendo razonamiento geométrico o solo validación numérica sobre una instancia concreta de coordenadas?
Para responder, primero hay que ver qué problema resuelve realmente el paper.
Qué problema resuelve realmente el paper
CodePlot-CoT se centra en un fenómeno de base: la memoria de trabajo espacial de los modelos multimodales es inestable en problemas matemáticos.
En concreto, el modelo puede entender el enunciado y producir una cadena de razonamiento estándar, pero cuando depende de estados geométricos intermedios, empieza a desviarse.
Eso se refleja en:
- líneas auxiliares inconsistentes entre pasos,
- relaciones espaciales olvidadas,
- pasos posteriores apoyados en estructuras que no existen.
MathCanvas responde con bocetos internos, formando una CoT visual (Visual Chain-of-Thought).
CodePlot-CoT toma otra vía: en vez de pedirle al modelo que imagine una figura, lo pone a operar en un entorno gráfico real y ejecutable.
Es decir, externaliza la "figura pensada" hacia Python.
Clave técnica: hacer que el modelo escriba matplotlib
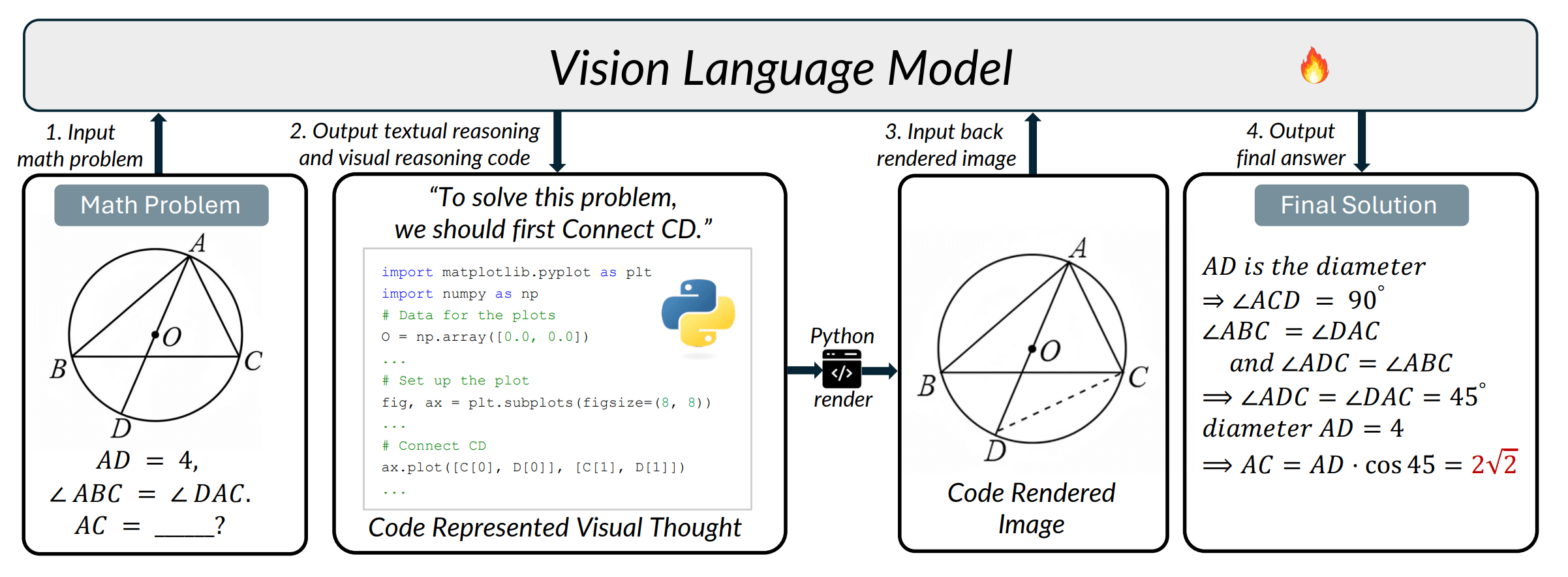
En un ejemplo del paper, el modelo da este paso:
"Conectar C y D primero"
Y en vez de continuar con texto, emite código Python:
ax.plot([C[0], D[0]], [C[1], D[1]])
El flujo completo es:
razonamiento textual -> generación de código de trazado -> render de imagen -> reentrada al modelo -> continuación del razonamiento
Así, el estado intermedio del razonamiento deja de existir solo en tokens o latentes y pasa a existir en un entorno externo ejecutable.
Esto trae beneficios inmediatos:
1. Estado espacial más estable
El modelo depende del entorno y no solo de la memoria (similar a agentes con herramientas).
2. Mejor consistencia visual
Disminuye el típico "derrape" de diagramas multimodales.
3. Escalabilidad de datos
El paper construye Math-VR (178 mil problemas), convirtiendo "figura -> código -> razonamiento" en señal supervisada.
Es una estrategia típica de visión por computador: no obligar al modelo a imaginar el mundo, sino entrenarlo con un mundo operativo.
Hasta aquí, el trabajo es elegante. Pero hay un límite directo.
Pregunta clave: ¿realmente entiende geometría?
Volvamos a la línea:
ax.plot([C[0], D[0]], [C[1], D[1]])
Eso significa: dibujar un segmento en un plano de coordenadas.
Pero el razonamiento geométrico necesita algo más.
En geometría, "unir C y D" no es solo dibujar, sino una operación de construcción:
- ¿CD es una cuerda?
- ¿CD es una bisectriz?
- ¿CD es perpendicular a una recta dada?
- ¿CD une intersecciones de dos circunferencias?
Ahí está la fuente del razonamiento.
Matplotlib expresa apariencia visual. La geometría exige restricciones relacionales.
Por tanto, la estructura intermedia sigue siendo "parece correcto", no "debe ser verdadero".
Pérdida de causalidad constructiva
La prueba geométrica depende de "por qué es verdadero", no de "si parece verdadero".
Por ejemplo, construcción: bisectriz -> ángulos iguales es una relación lógica.
En el razonamiento basado en render, eso se convierte en medir ángulos y ver que son aproximadamente iguales.
Son cosas distintas:
| Tipo | Naturaleza |
|---|---|
| Construcción geométrica | Necesaria |
| Instancia numérica | Contingente |
El esquema de CodePlot-CoT es:
generar una instancia de coordenadas -> mirar la imagen -> concluir
En matemáticas, eso es validación de una sola instancia. Pero un enunciado geométrico exige validez para todas las configuraciones, y el modelo solo ve un mundo de muestra.
Verificación visual vs prueba matemática
Aquí se distinguen dos paradigmas:
| CodePlot-CoT | Prueba geométrica | |
|---|---|---|
| Criterio de decisión | Parece válido | Necesariamente válido |
| Método | Experimento | Derivación |
| Naturaleza | Razonamiento empírico | Razonamiento deductivo |
CodePlot-CoT es, en la práctica, una "IA de experimento geométrico", no una "IA de prueba geométrica".
Responde a "¿esta imagen respalda la conclusión?" y no a "¿la conclusión es válida en un sistema axiomático?".
¿Por qué no llega a AlphaGeometry?
CodePlot-CoT de HKU ofrece gráficos ejecutables; AlphaGeometry de Google ofrece pruebas derivables.
Entre ambos falta una capa: la capa de objetos geométricos.
Concretamente:
- ¿un punto es intersección o punto libre?
- ¿una recta es bisectriz o simple segmento de unión?
- ¿una circunferencia está definida de forma única por tres puntos o dibujada arbitrariamente?
No es un problema visual, sino de modelado estructural matemático.
Si colocamos las rutas en un eje:
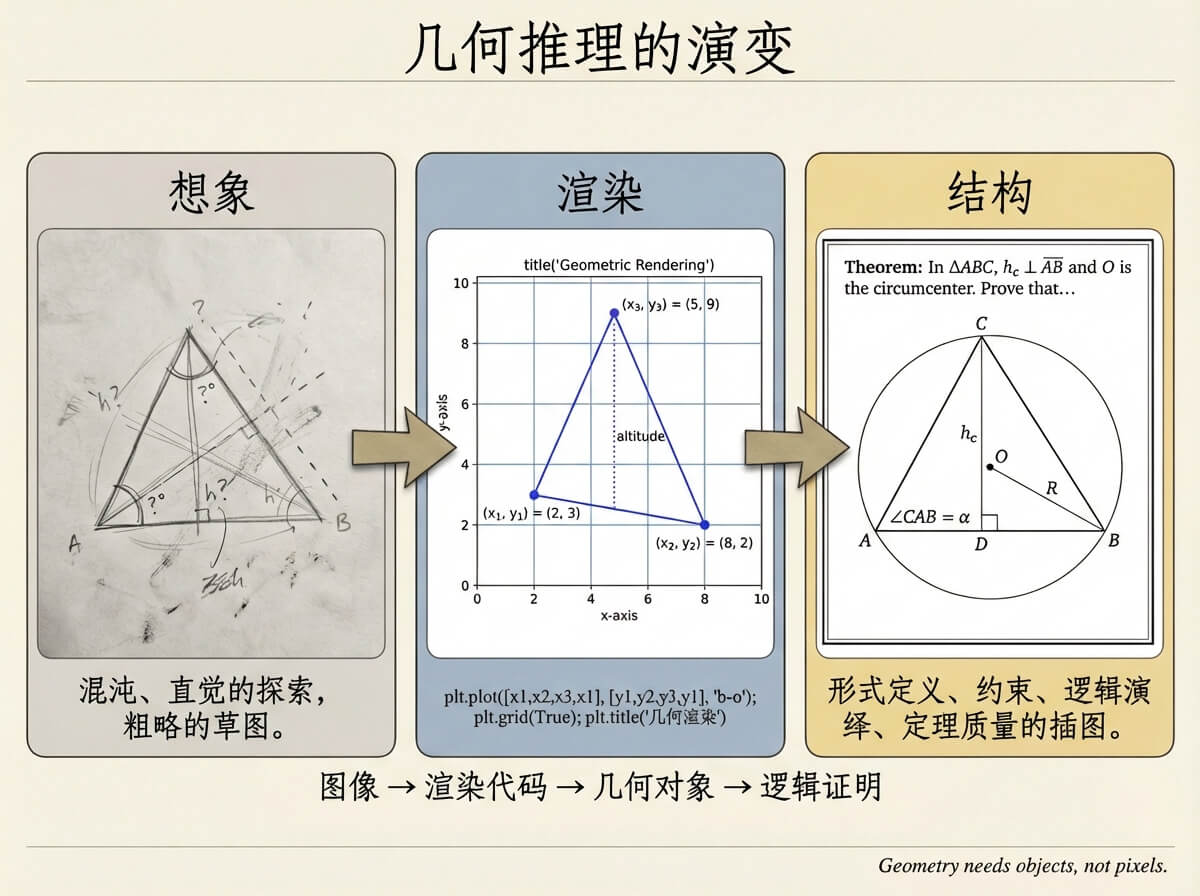
imagen -> código de render -> objetos geométricos -> prueba lógica
CodePlot-CoT se queda en la capa 2, AlphaGeometry está en la capa 4, y la capa 3 es precisamente donde más opera un humano al resolver: la construcción geométrica.
Al resolver geometría, rara vez empezamos por la prueba formal y tampoco nos quedamos en la imagen. Operamos sobre objetos: trazamos perpendiculares, tomamos intersecciones, construimos circunferencias por puntos, construimos bisectrices.
Ese paso no es puramente visual ni prueba final, pero determina si todo el razonamiento posterior puede sostenerse.
Cierre
En mi propio trabajo, Dino-GSP, estoy intentando aislar exactamente esta capa intermedia.
No se trata de "hacer que el modelo dibuje" ni de "forzar prueba formal directa", sino de hacer que opere sobre objetos geométricos.
La salida del modelo no es ax.plot(...), ni Therefore AB ⟂ CD, sino operaciones como:
PerpLine(<Line>, <Point>) # Trazar una perpendicular por un punto exterior
Intersection(Circle(O, 2), Line(2, 3)) # Obtener todas las intersecciones de círculo y recta
Cuando la representación intermedia pasa a ser restricciones sobre objetos, cambian muchas cosas:
- la figura puede generarse de forma estable sin depender de una sola instancia de coordenadas,
- las relaciones pueden verificarse directamente en lugar de medirse visualmente,
- el razonamiento puede formar una cadena formal en lugar de una inferencia empírica.
Desde esta perspectiva, CodePlot-CoT importa no porque simplemente "resuelva mejor matemáticas", sino porque demuestra que el razonamiento visual necesita un espacio de trabajo intermedio externo.
Es decir, el cuello de botella del LLM no es "no saber razonar matemáticamente", sino "no tener un espacio de trabajo para construir modelos matemáticos".
CodePlot-CoT ofrece un tipo de espacio de trabajo, pero todavía no es un espacio matemático.
Lo que la geometría probablemente necesita es un lenguaje geométrico operable.