前言
上一篇寫 MathCanvas 深度解析 的時候,我的總結觀點是: 大模型在幾何上不穩定,並不是因為看不懂圖,而是因為沒有穩定的中間結構可以操作。
一些研究工作開始讓模型畫出來再想。
例如 MathCanvas 的做法,讓模型在內部生成草圖,再基於草圖推理。
寫完那篇後,有讀者問我:
既然視覺中間步驟這麼重要,為什麼不直接讓模型把圖真的畫出來?
找了一下相關研究,果然有,看到 HKU 的 CodePlot-CoT,他們就是這麼做的。
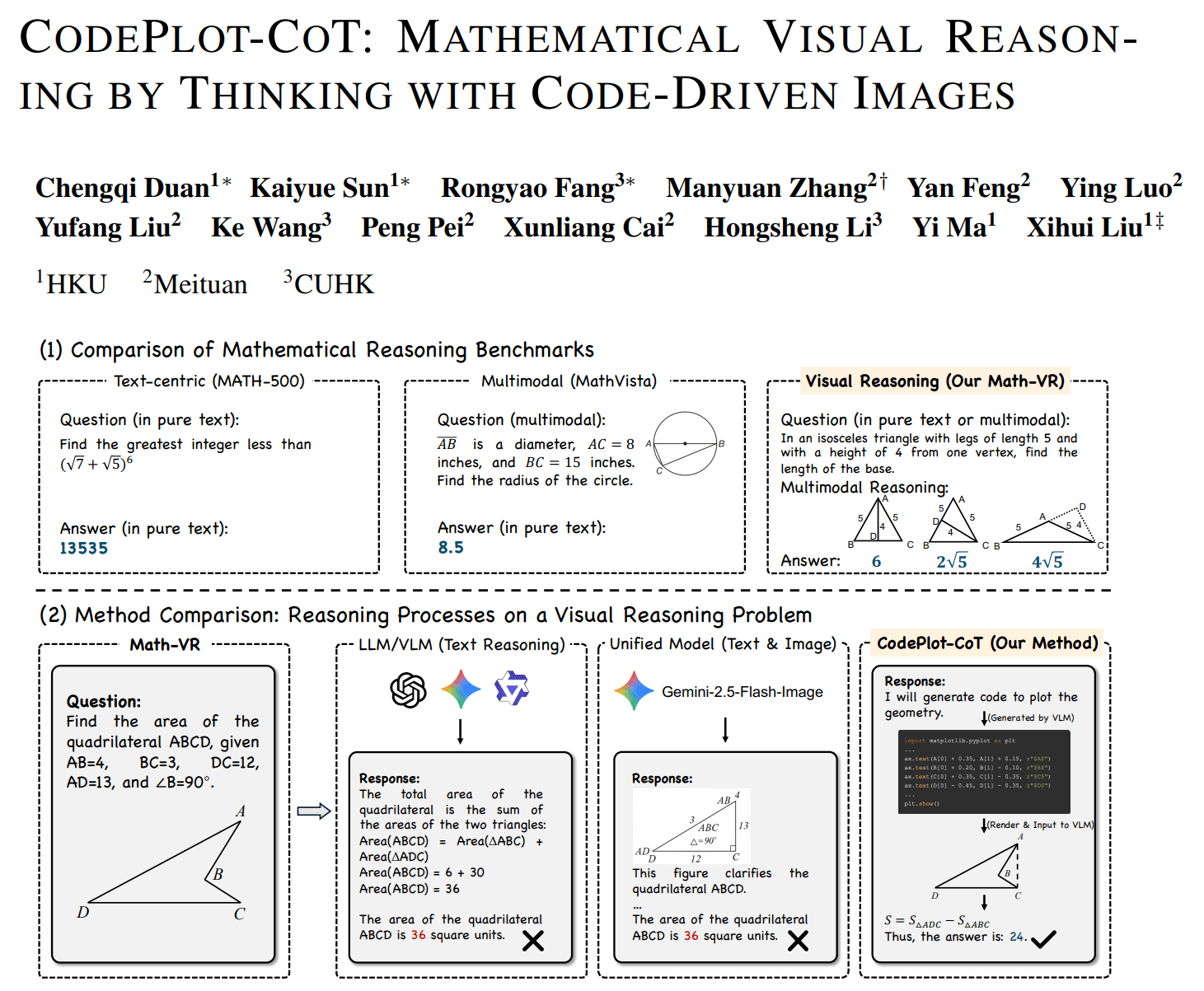
模型不再「腦補」輔助線,而是寫 python matplotlib,把輔助線真的畫出來,再繼續解題。
聽起來非常合理吧,如果視覺推理不穩定,那就給模型一個可執行的視覺世界。
但新的問題也隨之出現:
當模型開始「寫圖形程式碼」時,它到底是在進行幾何推理,還是只是在一個具體座標實例上做數值驗證?
要回答這個問題,得先看論文到底在解決什麼。
論文真正要解決的問題
CodePlot-CoT 聚焦的是一個底層現象:多模態模型在數學題中空間工作記憶不穩定。
具體來說,模型可以讀懂題意,也能寫出標準推理鏈,但一旦依賴圖形中間狀態,推理就開始漂移。
這表現在:
- 輔助線前後不一致
- 空間關係被遺忘
- 後續步驟依賴一個並不存在的結構
上篇分享的 MathCanvas 的答案是在模型內部生成草圖,形成視覺 CoT(Visual Chain-of-Thought)。
而 CodePlot-CoT 選擇了另一條路,與其讓模型想像圖,不如讓模型操作一個真實可執行的圖形環境。
換句話說,他們把「思考中的圖」外包給 Python。
技術關鍵:讓模型寫 matplotlib
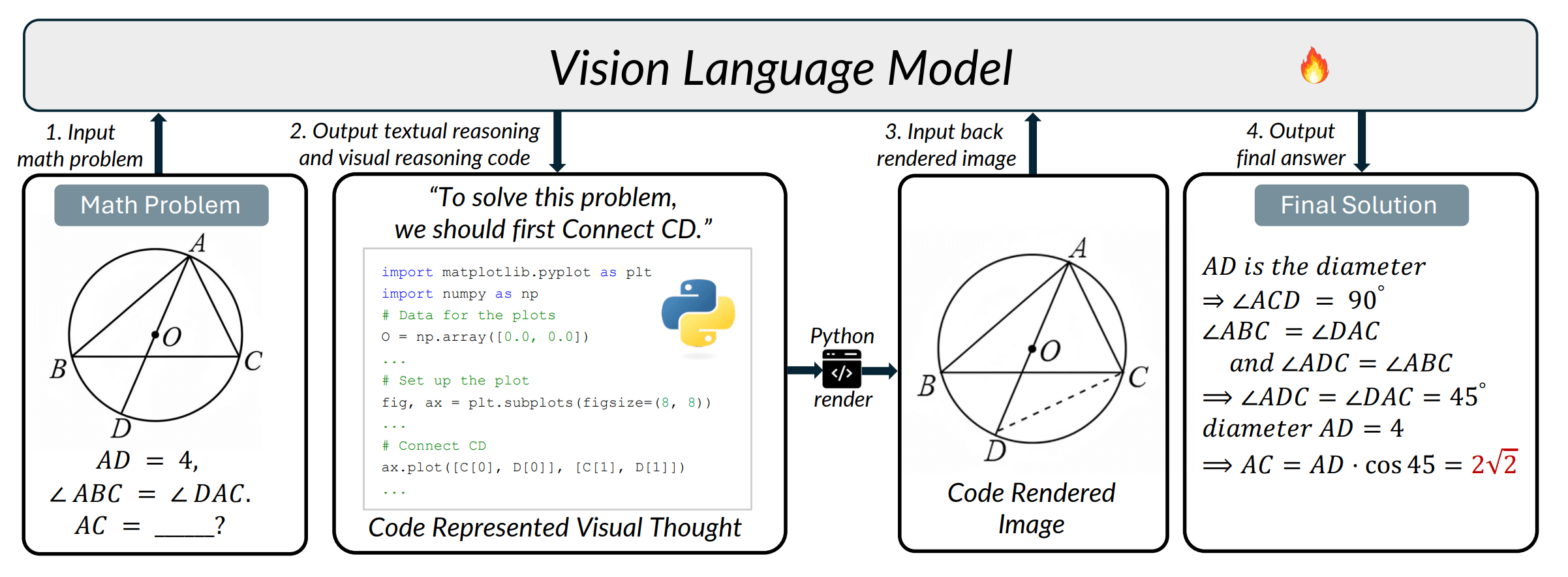
論文中的一個示例,模型在推理過程中給出一步:
「先連接 CD」
然後不是繼續寫文字,而是直接輸出 python 程式碼:
ax.plot([C[0], D[0]], [C[1], D[1]])
整個流程就是:
文本推理 -> 生成繪圖程式碼 -> 渲染圖像 -> 再輸入模型 -> 繼續推理
也就是說,模型的「思維中間狀態」不再存在於 token 或 latent,而存在於一個可執行環境中的外部世界。
這帶來幾個立刻可見的好處:
1. 空間狀態穩定
模型不再依賴記憶,而依賴環境(類似 agent 使用工具)。
2. 視覺一致性提高
多模態模型常見的「圖變形」問題消失。
3. 數據可規模化
論文構建了 Math-VR 數據集(17.8 萬題),把「圖 -> 程式碼 -> 推理」變成監督訊號。
這是一個非常典型的計算機視覺團隊思路:不讓模型學會想像世界,而是給模型訓練一個世界。
到這裡為止,這篇論文其實相當漂亮,但細想也有很直接的問題。
關鍵問題:它真的理解了幾何嗎?
我們看回那句程式碼:
ax.plot([C[0], D[0]], [C[1], D[1]])
這句話表達的含義是:在座標平面畫一條線段。
但幾何推理需要的不是這個。
幾何裡,「連 CD」並不是畫線,而是一個構造操作:
- CD 是弦?
- CD 是角平分線?
- CD 與某線垂直?
- CD 是兩圓交點連線?
這些才是推理的來源。
matplotlib 表達的是圖像外觀,幾何推理需要的是關係約束。
也就是說,這個中間結構仍然停留在「看起來像」,而不是「必然成立」。
構造因果的丟失
幾何證明依賴的是「為什麼成立」,而不是「是否成立」。
例如 構造:角平分線 -> 等角,這是邏輯關係。
但在渲染圖中變成 測量角度 ≈ 相等。
這兩者本質不同:
| 類型 | 性質 |
|---|---|
| 幾何構造 | 必然 |
| 數值實例 | 偶然 |
CodePlot-CoT 的推理方式是:
生成一個座標實例 -> 看圖 -> 得出結論
這在數學上叫單實例驗證,問題是幾何命題要求對所有配置成立,而模型看到的只是一個樣本世界。
視覺驗證 vs 數學證明
到這裡可以抽象成兩種推理範式:
| CodePlot-CoT | 幾何證明 | |
|---|---|---|
| 判斷依據 | 看起來成立 | 必然成立 |
| 方法 | 實驗 | 推導 |
| 本質 | 經驗推理 | 演繹推理 |
CodePlot-CoT 實際上做的是「幾何實驗 AI」,而不是「幾何證明 AI」。
它在回答「這張圖像是否支持這個結論」,而不是「這個結論是否在公理系統中成立」。
為什麼它到不了 AlphaGeometry?
HKU CodePlot-CoT 提供了可執行圖形;Google AlphaGeometry 提供了可推導證明。
但中間少了一層東西:幾何對象本身。
具體來說:
- 點是交點還是自由點?
- 線是角平分線還是連接線?
- 圓是過三點唯一圓還是隨便畫的圓?
這不是視覺問題,而是數學結構建模問題。
如果把三種路線放在一條軸上:
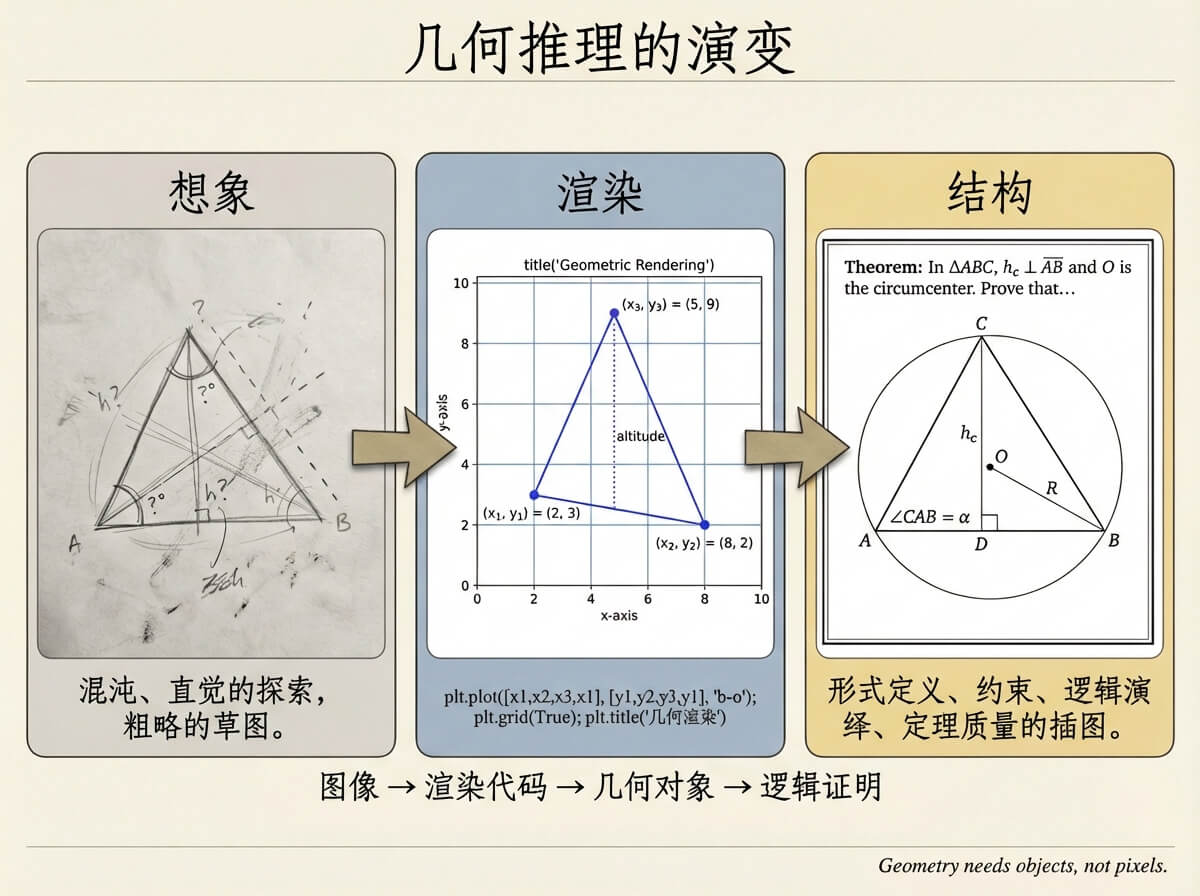
圖像 -> 渲染程式碼 -> 幾何對象 -> 邏輯證明
CodePlot-CoT 停在第二層,AlphaGeometry 在第四層,而第三層其實才是人類解題最常操作的部分:構造圖形。
我們解幾何題時,很少一開始就寫證明,也不會只看圖像,而是在操作對象:作垂線、取交點、過點作圓、作角平分線……
這一步既不是視覺,也不是證明,但決定了後面一切推理是否成立。
寫在最後
我自己在做的大角幾何(Dino-GSP),其實就是在嘗試把這一層單獨抽出來。
不是讓模型畫圖,也不是讓模型直接證明,而是讓模型操作幾何對象本身。
模型輸出的不是 ax.plot(...),也不是 Therefore AB ⟂ CD,而是:
PerpLine(<Line>, <Point>) # 過直線外一點作垂線
Intersection(Circle(O, 2), Line(2, 3)) # 取圓和直線的所有交點
一旦中間結構變成對象約束,很多事情就會改變:
- 圖形可以穩定生成,而不是依賴單個座標實例
- 關係可以直接驗證,而不是視覺測量
- 推理可以建立鏈條,而不是經驗判斷
從這個角度看,CodePlot-CoT 很重要,重要性不在「解數學題更強」,而在它證明視覺推理需要外部中間狀態。
也就是說,LLM 的問題不是不會數學推理,而是沒有工作空間建立數學模型。
CodePlot-CoT 提供了一種工作空間,只是這個空間還不是數學空間。
而幾何真正需要的,可能是一套可以被操作的圖形語言。