前言
上一篇写 MathCanvas 深度解析 的时候,我的总结观点是: 大模型在几何上不稳定,并不是因为看不懂图,而是因为没有稳定的中间结构可以操作。
一些研究工作开始让模型画出来再想。
比如 MathCanvas 的做法,让模型在内部生成草图,再基于草图推理。
写完那篇后,有读者问我:
既然视觉中间步骤这么重要,为什么不直接让模型把图真的画出来?
找了下相关的研究,果然有,看到 HKU 的 CodePlot-CoT,他们就是这么做了。
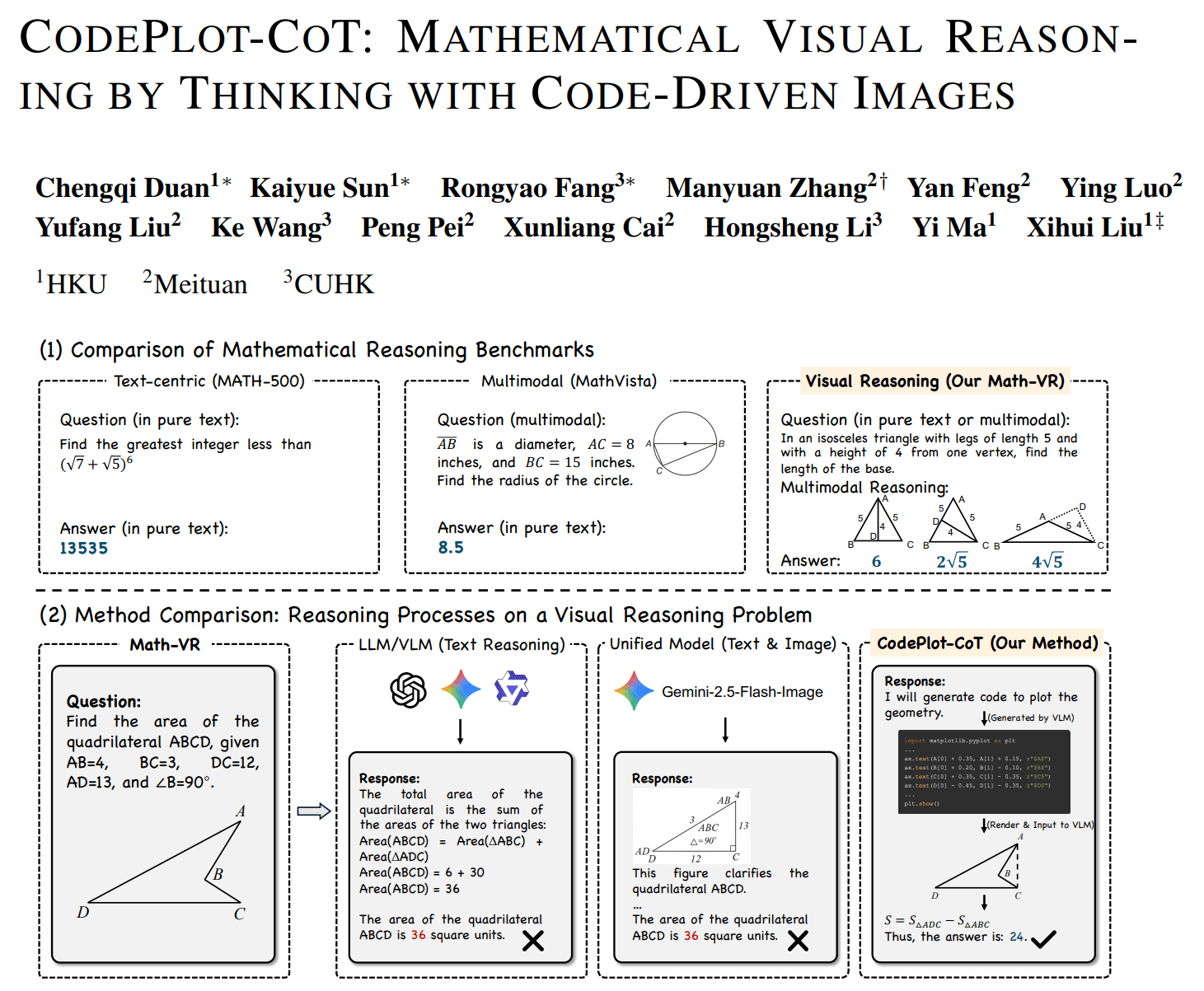
模型不再“脑补”辅助线,而是写 python matplotlib,把辅助线真的画出来,再继续解题。
听起来非常合理吧,如果视觉推理不稳定,那就给模型一个可执行的视觉世界。
但新的问题也随之出现:
当模型开始“写图形代码”时,它到底是在进行几何推理,还是只是在一个具体坐标实例上做数值验证?
要回答这个问题,得先看论文到底在解决什么。
论文真正要解决的问题
CodePlot-CoT 聚焦关注的是一个底层现象:多模态模型在数学题中空间工作记忆不稳定。
具体来说,模型可以读懂题意,也能写出标准推理链,但一旦依赖图形中间状态,推理就开始漂移。
这表现在:
- 辅助线前后不一致
- 空间关系被遗忘
- 后续步骤依赖一个并不存在的结构
上篇分享的 MathCanvas 的答案是在模型内部生成草图,形成视觉 CoT(Visual Chain-of-Thought)。
而 CodePlot-CoT 选择了另一条路,与其让模型想象图,不如让模型操作一个真实可执行的图形环境。
换句话说,他们把“思考中的图”外包给 Python。
技术关键:让模型写 matplotlib
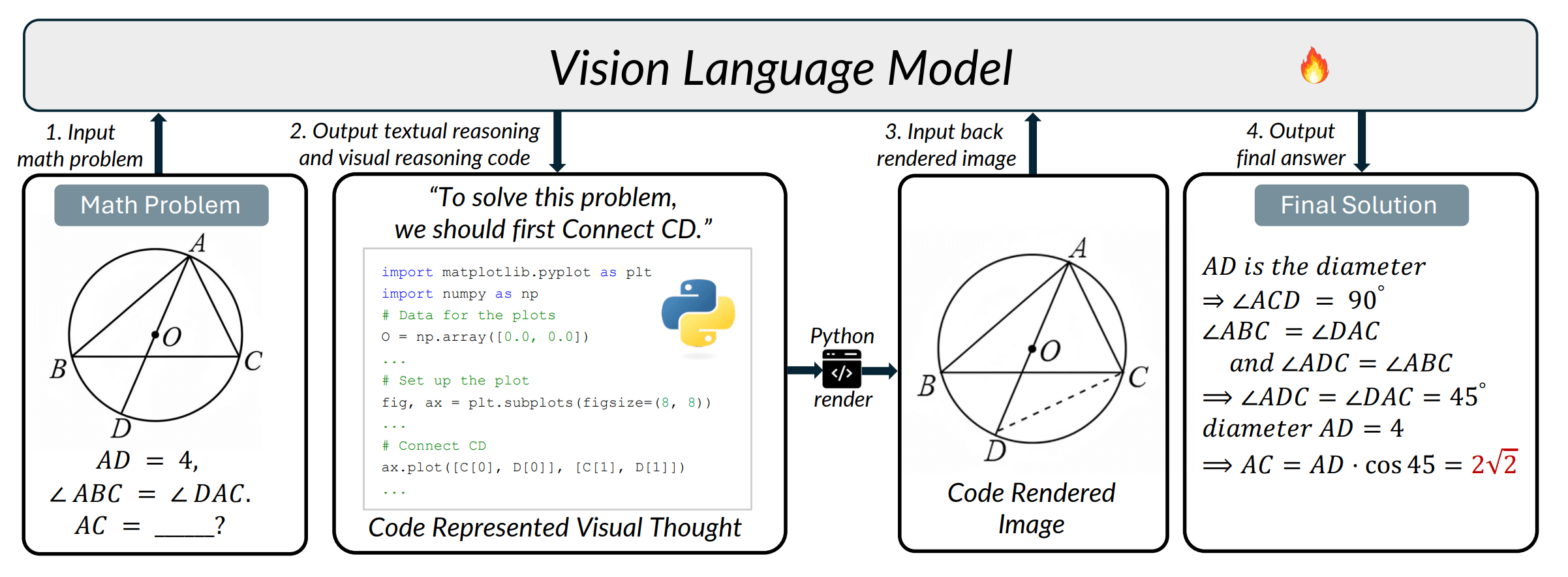
论文中的一个示例,模型在推理过程中给出一步:
“先连接 CD”
然后不是继续写文字,而是直接输出 python 代码:
ax.plot([C[0], D[0]], [C[1], D[1]])
整个流程就是:
文本推理 -> 生成绘图代码 -> 渲染图像 -> 再输入模型 -> 继续推理
也就是说,模型的“思维中间状态”不再存在于 token 或 latent,而存在于一个可执行环境中的外部世界。
这带来几个立刻可见的好处:
1. 空间状态稳定
模型不再依赖记忆,而依赖环境(类似 agent 使用工具)。
2. 视觉一致性提高
多模态模型常见的“图变形”问题消失。
3. 数据可规模化
论文构建了 Math-VR 数据集(17.8 万题),把“图 -> 代码 -> 推理”变成监督信号。
这是一个非常典型的计算机视觉团队思路:不让模型学会想象世界,而是给模型训练一个世界。
到这里为止,这篇论文其实相当漂亮,但细想也有很直接的问题。
关键问题:它真的理解了几何吗?
我们看回那句代码:
ax.plot([C[0], D[0]], [C[1], D[1]])
这句话表达的含义是:在坐标平面画一条线段。
但几何推理需要的不是这个。
几何里,“连 CD”并不是画线,而是一个构造操作:
- CD 是弦?
- CD 是角平分线?
- CD 与某线垂直?
- CD 是两圆交点连线?
这些才是推理的来源。
matplotlib 表达的是图像外观,几何推理需要的是关系约束。
也就是说,这个中间结构仍然停留在“看起来像”,而不是“必然成立”。
构造因果的丢失
几何证明依赖的是“为什么成立”,而不是“是否成立”。
比如 构造:角平分线 -> 等角,这是逻辑关系。
但在渲染图中变成 测量角度 ≈ 相等。
这两者本质不同:
| 类型 | 性质 |
|---|---|
| 几何构造 | 必然 |
| 数值实例 | 偶然 |
CodePlot-CoT 的推理方式是:
生成一个坐标实例 -> 看图 -> 得出结论
这在数学上叫单实例验证,问题是几何命题要求对所有配置成立,而模型看到的只是一个样本世界。
视觉验证 vs 数学证明
到这里可以抽象成两种推理范式:
| CodePlot-CoT | 几何证明 | |
|---|---|---|
| 判断依据 | 看起来成立 | 必然成立 |
| 方法 | 实验 | 推导 |
| 本质 | 经验推理 | 演绎推理 |
CodePlot-CoT 实际上做的是“几何实验 AI”,而不是“几何证明 AI”。
它在回答“这张图像是否支持这个结论”,而不是“这个结论是否在公理系统中成立”。
为什么它到不了 AlphaGeometry?
HKU CodePlot-CoT 提供了可执行图形;Google AlphaGeometry 提供了可推导证明。
但中间少了一层东西:几何对象本身。
具体来说:
- 点是交点还是自由点?
- 线是角平分线还是连接线?
- 圆是过三点唯一圆还是随便画的圆?
这不是视觉问题,而是数学结构建模问题。
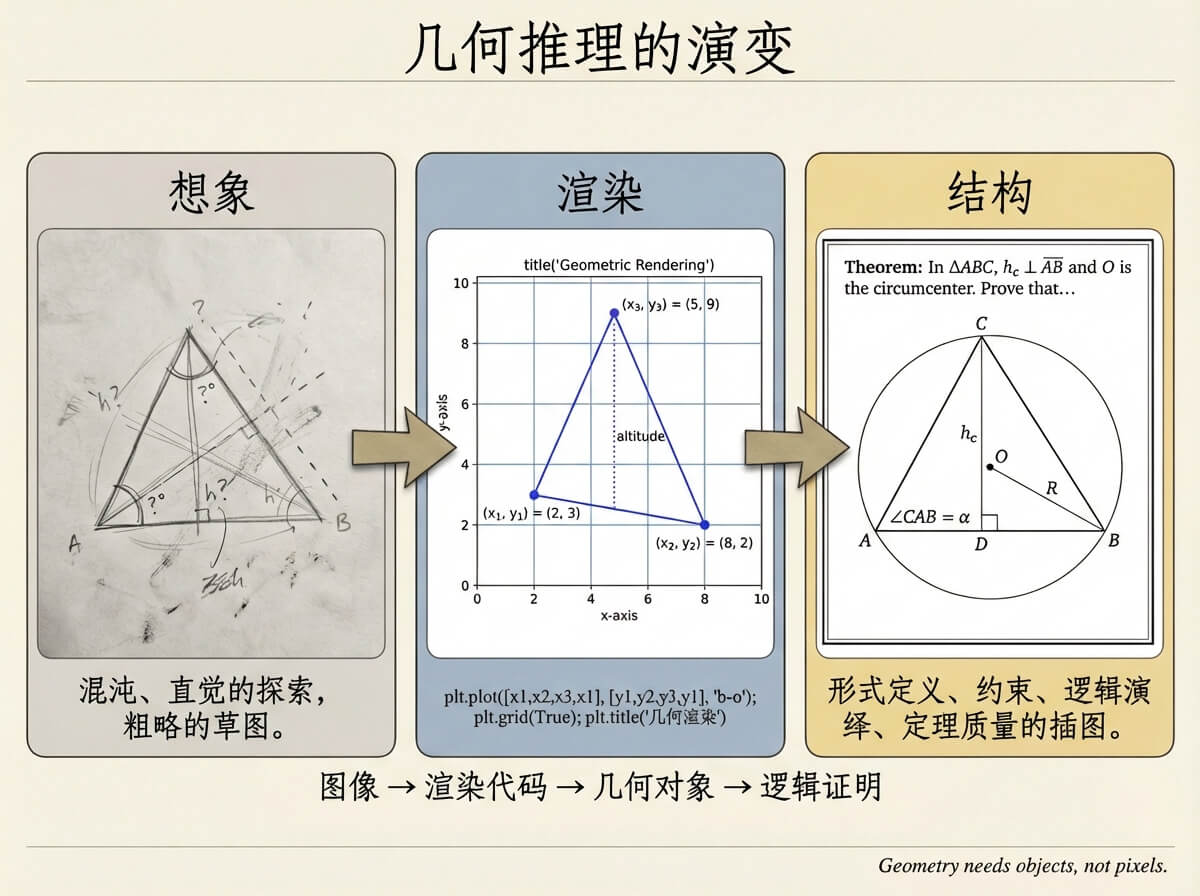
如果把三种路线放在一条轴上:
图像 -> 渲染代码 -> 几何对象 -> 逻辑证明
CodePlot-CoT 停在第二层,AlphaGeometry 在第四层,而第三层其实才是人类解题最常操作的部分:构造图形。
我们解几何题时,很少一开始就写证明,也不会只看图像,而是在操作对象:作垂线、取交点、过点作圆、作角平分线……
这一步既不是视觉,也不是证明,但决定了后面一切推理是否成立。
写在最后
我自己在做的大角几何(Dino-GSP),其实就是在尝试把这一层单独抽出来。
不是让模型画图,也不是让模型直接证明,而是让模型操作几何对象本身。
模型输出的不是 ax.plot(...),也不是 Therefore AB ⟂ CD,而是:
PerpLine(<Line>, <Point>) # 过直线外一点作垂线
Intersection(Circle(O, 2), Line(2, 3)) # 取圆和直线的所有交点
一旦中间结构变成对象约束,很多事情就会改变:
- 图形可以稳定生成,而不是依赖单个坐标实例
- 关系可以直接验证,而不是视觉测量
- 推理可以建立链条,而不是经验判断
从这个角度看,CodePlot-CoT 很重要,重要性不在“解数学题更强”,而在它证明视觉推理需要外部中间状态。
也就是说,LLM 的问题不是不会数学推理,而是没有工作空间建立数学模型。
CodePlot-CoT 提供了一种工作空间,只是这个空间还不是数学空间。
而几何真正需要的,可能是一套可以被操作的图形语言。